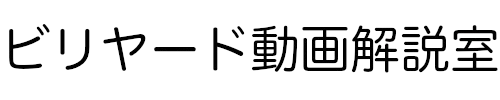本記事から、極意シリーズを展開していきたいと思います!(すぐ終わるかもしれませんが笑)
ここには、私がビリヤードを実際にやるときに考えていることを極意として、
文章に起こしていきたいと思います🎵
初級者・中級者の方は参考に、上級者の方は暖かく見守っていただけると嬉しいです笑
そして、ビリヤードはスポーツなので、記事だけ読んでも絶対できないです!
なので、この記事を読んだら、ビリヤード場に行ってたくさん練習しましょう笑
球の力加減に影響するもの
それでは本題に入りたいと思います。
今回のテーマは「球の力加減」です。
極意について説明する前に、まずはこの力加減に作用する要因を考えたいと思います。
- キューのテイクバック(インパクト前にどれだけキューを引くか)
- キューを出す時のスピード
まずこれを見ると、「キューを持っている手の力は関係ないの?」というご質問はありそうですね。
そして、回答としては関係ないです!(ゼロじゃないかもですが)
みなさん一回は見たことがある振り子運動がビリヤードでやっていることなのです!!!
動画を貼っておくので、これを見ていただくと、端の球を持ち上げて振り下ろしているのがまさに腕の役割なのです!

したがって力加減をコントロールするには、振り子の位置を高くする(テイクバックを大きくとる)か、キューのスピードを上げるのどちらかになります。
どちらをコントロールすべきなのか?
では、テイクバックとキュースピードはどちらをコントロール、もしくは両方コントロールすべきなのでしょうか?
私の回答としては、テイクバックでコントロールして、キュースピードは一定にするべきだと思います。
その理由については、以下があります。
- テイクバックの取る量である程度力加減が可視化できる。
キュースピードだと目には見えない。 - キュースピードの増減は、キューをまっすぐ出す観点でずれる要因になる。
また、球の撞点(真ん中とか左右上下とか)もズレる要因になる。
一方、テイクバックはまっすぐ出すことにも球の撞点にも影響しない。
と、ここまで言ってきましたが、ここら辺のことはビリヤード教本にも数々の先輩方のブログやYouTubeなどにも上がっているため、そこまで言っていることに大差はないと思います。
ですが、同じことを繰り返していうということは、重要なことだからなので、この点はしっかり押さえておきましょう。
力加減の目安
力加減をコントロールするものが分かった上で、どのように力を出せば良いかを解説していきたいと思います。ここからはオリジナルだと思っているので、みなさん楽しんで読んでください!
その前に
一つ前提知識が必要ですので、説明させてください。
みなさんは、ビリヤード台の広さがどうなっているかご存知でしょうか?
何メートルなどは私も正確には把握していませんが笑
実はビリヤード台というのは、正方形を二つ合わせてできた長方形なのです!!!
これがここからの解説にめちゃくちゃ重要ですので、この情報だけは覚えておきましょう。
力加減の基準
それではここから極意に迫っていきたいと思います!
まず力加減については、絶対的なものではなく、相対的なものになります。
すなわち一つ自分の中で確かな指標を用意しておくことが必要になります。私はそれをバンキングの力加減においています。ただし、この基準は自分で好きなものを用意して大丈夫です。
力加減を計算してみよう!
ここからはいくつか思考問題をやってみて、力加減をどう考えるかご説明します!
さて、下図のように手前の長クッションから奥の長クッションに当てて、もう一度同じ位置に戻してくるには、どれくらいの力加減になるでしょうか?
この問いに対して、基準をバンキングだとして、バンキングよりどれくらい弱いのか、または強いのか、または同じなのかという回答を考えることができます!

正解は、、、
バンキングの半分くらいの力加減です!(正確には半分よりはやや強い)
なんでこんなことがわかるのかですが、ここで前提のビリヤード台は同じ正方形二つからできているという知識が重要になってきます。
バンキングの動きについて先ほどの図でめちゃくちゃざっくり言うと、左の短クッション→右の短クッション→左の短クッションになりますね。つまり、長い辺を2辺分ということです。
続いて、今の問題の長クッションの折り返しは短い辺を2辺分です。
ビリヤード台は正方形が二つなので、短い辺が2辺分というのは、言い換えると、長い辺を1辺分ですね。ということは、バンキングが長い辺2辺分だったので、今の問題はその半分であると言えるのです!
これを実践でやる時には、バンキングでやっているテイクバックの半分の長さでテイクバックすれば、理論上は想定の力加減でつけると思います。

ではもう一問やってみましょう。
下図の配置になった時、どの力加減であれば、テーブルセンターに持ってくることができるでしょうか?なお、1番のシュートの厚みは球の半分とします。
いきなり難しいですね。でも今は分からなくても大丈夫です。
仮にここで理論が分かっても実践でやってみたほうがわかることも多いので、ぜひビリヤード場で試してみてください。
この問題の正解はバンキングの半分より少し強いが正解です。
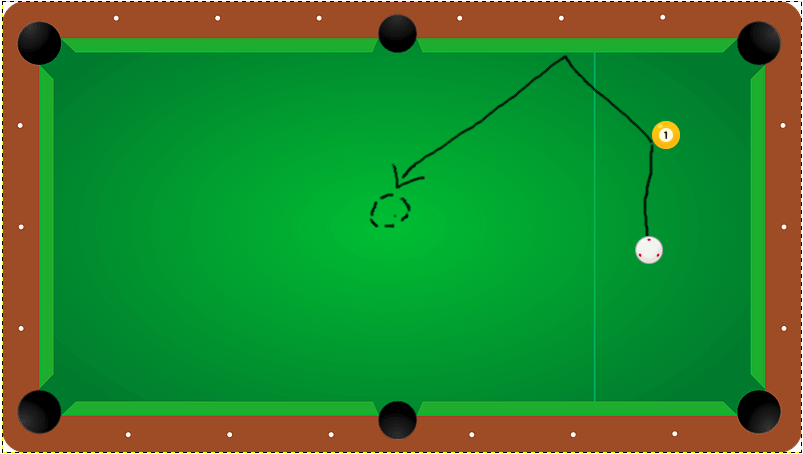
先ほどに無い要素として、①的球がある、②斜めに動くというのがありますね。
①的球については、手球と的球がどれだけ当たったかによって、力の残り方が変わります。
極端な例で言えば、もし1番に厚く当たると、手球はその場に残り、その力の分だけ1番が動きます。逆にとても薄いと手球の力は残り、1番は少ししか動きません。
今回は、半分の厚みとありますので、半分の力を持っていかれます。
②斜めの移動ですが、ここは三平方の定理が必要です。正方形を半分に割った直角三角形の斜辺は、他の1辺の大体1.4倍(ルート2)です。
これらをまとめて書くと、下図のようになります。
手球の動きだけで言えば、計算上5.2となりますが、1番に半分当たるので、力が半減されます。
そのため、10.4の力が必要になるので、バンキング半分(8.0)よりやや強い力加減が必要とされるという訳です。
実践での利用方法
この説明を見ると、こんなの毎回計算しないといけないの?となりそうですが、そうでは無いので、ご安心ください。
上でもみた通り、まず基準よりも強いのか、弱いのか、一緒くらいなのかは判断する必要があります。でもどれだけ計算したところで、テイクバックをバンキングより1.5倍くらい引いたり戻したりするのは感覚によるところなので、そこは練習によるところしか無いからです。
ただし、この計算の良いのは、練習でやっていない配置でも応用が効く点です。
なので、あとは基準さえ増やせばどんな配置であってもすぐに力加減を判断することができるようになります。
私の場合は、力の基準は短クッション1辺分、長クッション1辺分、長クッション1.5辺分(バンキング)、長クッション2辺分の4つがあるので、これだけあると、十分試合では困らないかと思います。
まとめ
この記事では球の力加減について説明していきました。思ったよりビリヤードって物理法則そのままですよね!ちなみに私は文系で物理の勉強もしていなかったので、文系の方でもビリヤードが好きなら問題なく吸収できると思います!!!
気になることやご質問があれば、X(@position_taro)までお気軽にどうぞ!